
Curso de regularización de Integrales de 13:30 a 18:30

La ingeniería de sistemas es una ciencia interdiciplinaria que se encarga del diseño, la programación, la implantación y el mantenimiento de sistemas. A diferencia de otras ramas de la ingeniería, esta disciplina no se ocupa de productos tangibles (los ingenieros civiles, por ejemplo, construyen edificios), sino de productos lógicos.
Por lo tanto, la ingeniería de sistemas implica el uso de nociones matemáticas que permitan concretar la aplicación tecnológica de las teorías de los sistemas. Se trata de una ciencia interdisciplinaria, que requiere de diversos conocimientos para plasmar sus diseños en la vida práctica.
La ingeniería de sistemas permite transformar una necesidad operativa en una descripción de los parámetros del rendimiento de un sistema, con su correspondiente configuración. Por otra parte, posibilita la integración de los parámetros técnicos relacionados de modo tal que las interfaces de programa y funcionales sean compatibles y se garantice el funcionamiento del sistema total.

La simulación es una técnica muy poderosa y ampliamente usada en las ciencias para analizar y estudiar sistemas complejos. En Investigaciones se formularon modelos que se resolvían en forma analítica. En casi todos estos modelos la meta era determinar soluciones óptimas. Sin embargo, debido a la complejidad, las relaciones estocásticas, etc., no todos los problemas del mundo real se pueden representar adecuadamente en forma de modelo. Cuando se intenta utilizar modelos analíticos para sistemas como éstos, en general necesitan de tantas hipótesis de simplificación que es probable que las soluciones no sean buenas, o bien, sean inadecuadas para su realización. En eso caso, con frecuencia la única opción de modelado y análisis de que dispone quien toma decisiones es la simulación. Simular, es reproducir artificialmente un fenómeno o las relaciones entrada-salida de un sistema. Esto ocurre siempre cuando la operación de un sistema o la experimentación en él son imposibles, costosas, peligrosas o poco prácticas, como en el entrenamiento de personal de operación, pilotos de aviones, etc.
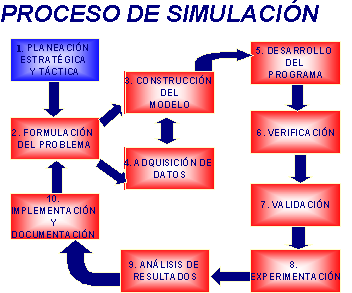
La simulación es la representación de un proceso o fenómeno mediante otro mas simple, que permite analizar sus características; Pero la simulación no es solo eso también es algo muy cotidiano, hoy en día, puede ser desde la simulación de un examen, que le hace la maestra a su alumno para un examen diagnóstico, la producción de textiles, alimentos, juguetes, construcción de infraestructuras por medio de maquetas, hasta el entrenamiento virtual de los pilotos de combate.

Dentro del calculo Integral o integración es un concepto fundamental del cálculo y del análisis matemático. Básicamente, una integral es una generalización de la suma de infinitos sumandos, infinitamente pequeños. El cálculo integral, encuadrado en el cálculo infinitesimal, es una rama de las matemáticas en el proceso de integración o antiderivación. Es muy común en la ingeniería y en la ciencia también; se utiliza principalmente para el cálculo de áreas y volúmenes de regiones y sólidos.
La integral definida de una función representa el área limitada por la gráfica de la función, en un sistema de coordenadas cartesianas con signo positivo cuando la función toma valores positivos y signo negativo cuando toma valores negativos.
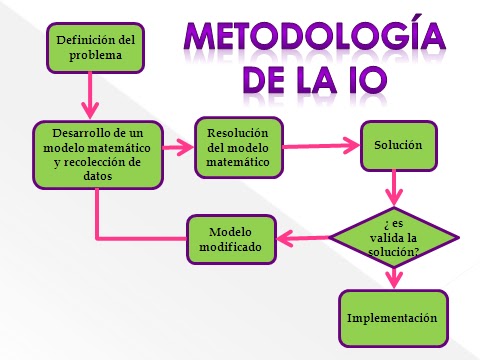
La investigación de operaciones se apoya en gran medida en la programación lineal la cual es el campo de la optimización matemática dedicado a maximizar o minimizar (optimizar) una función lineal, denominada función objetivo, de tal forma que las variables de dicha función estén sujetas a una serie de restricciones expresadas mediante un sistema de ecuaciones o inecuaciones también lineales. El método tradicionalmente usado para resolver problemas de programación lineal es el Método Simplex.
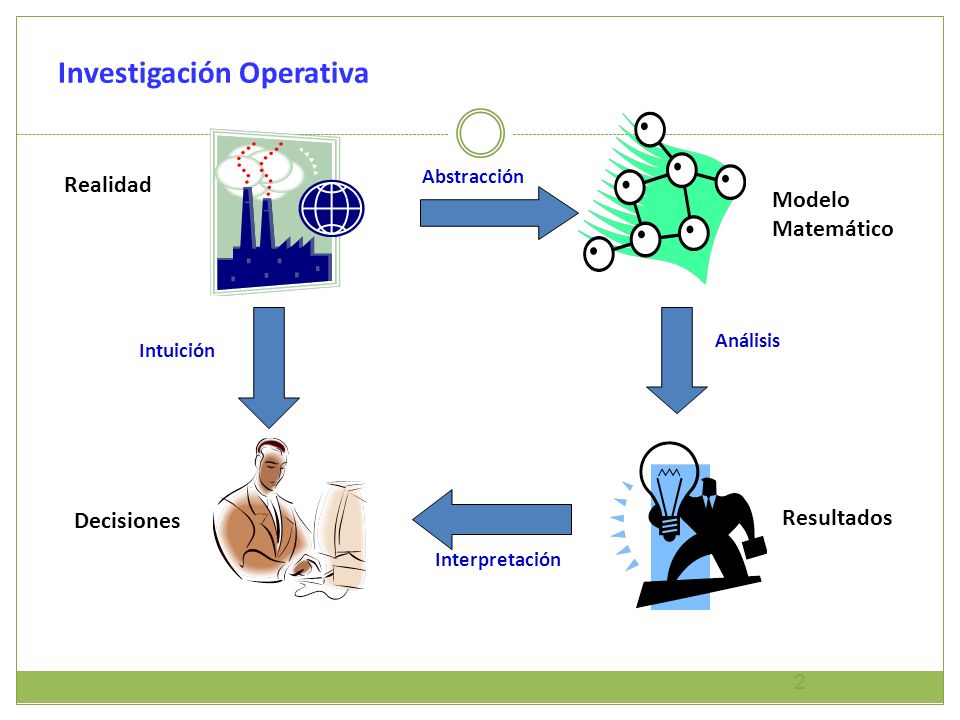
La investigación de operaciones también conocida como teoría de toma de decisiones o programación matemática es una ciencia interdisciplinaria que consiste en el uso de modelos matemáticos, estadística y algoritmos con objeto de realizar un proceso de toma de decisiones.
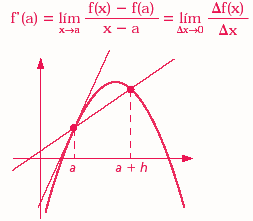
El cálculo diferencial es una parte del análisis matemático que consiste en el estudio de cómo cambian las funciones cuando sus variables cambian. El principal objeto de estudio en el cálculo diferencial es la derivada. Una noción estrechamente relacionada es la de diferencia
El estudio del cambio de una función es de especial interés para el cálculo diferencial, en concreto el caso en el que el cambio de las variables es infinitesimal, esto es, cuando dicho cambio tiende a cero (se hace tan pequeño como se desee). Y es que el cálculo diferencial se apoya constantemente en el concepto básico del límite. El paso al límite es la principal herramienta que permite desarrollar la teoría del cálculo diferencial y la que lo diferencia claramente del álgebra.